過剰間隙水圧の消散、浸透およびこれに伴う沈下、変形の連成解析(理論)
理論
Biotの多次元圧密方程式
地震継続時間中の間隙水圧および有効応力の取り扱い
要素特性と時間積分
土の構成式
不飽和領域の取り扱い
Biotの多次元圧密方程式
多次元圧密方程式を構成するには、応力変形に関する基礎方程式を満足する必要がある。全応力の釣り合い方程式は次式で表される。
σij,j+ρs bi=0 ----------(1)
ここに、σijは全応力、ρsは土の密度、biは単位質量当たりの物体力ベクトルで、σij,jの,jは直交座標jに関する偏微分を表す。
有効応力は全応力から間隙水圧を差し引いたものと定義されるが、不飽和領域では間隙圧としては間隙水圧と間隙空気圧が存在し、固相と合わせて厳密には3相系の問題として取り扱う必要が生じる。ここでは、間隙空気圧は取り扱わず間隙水圧のみ取り扱うこととし、有効応力を次式で表すものとする。
σij'=σij+χδij u ----------(2)
ここに、σij'は有効応力、δijはクロネッカーのデルタ、uは間隙水圧、χは飽和度に関するパラメーターで飽和の場合χ=1、不飽和の場合0<χ<1である。不飽和領域での浸透流に関しては、比透水係数および比水分容量を用いる手法を適用する。
上式の間隙水圧を全水頭hと水の単位体積重量をγw用いて表し、式(1)に代入すると、
σij,'j +χδijγw h ,j +ρs bi=0 ----------(3)
となる。有効応力に基づく応力〜ひずみ関係は、
σij' = Cijkl εkl ------------(4)
で表される。ここに、Cijklは弾性係数、εklはひずみテンソルで、次式で表される。
εkl =(1/2)(δk,l +δl,k) ------------(5)
ここに、δkは変位ベクトルである。
一方、不飽和領域を含めた浸透流に関して、Darcyの法則は次式で表される。
Vi =-k(θ)h ,i ------------(6)
ここに、Viは流速ベクトル、k(θ)は体積含水率θの関数としての透水係数である。質量保存則は、
−(ρfVi),i=(∂/∂t)(ρfθ) ------------(7)
で表される。ここに、ρfは間隙流体の密度である。
式(4)、(5)を式(3)に代入すると次式が得られる。
{1/2 Cijkl(δk,l +δl,k)+χδijγw h } ,j+ρs bi=0 ------------(8)
また、式(6)を式(7)に代入し、間隙流体の密度変化を無視すると次式のように表される。
{ k(θ)h ,i},i−(∂δi,i/∂t)Sr−C(ψ)(∂h/∂t)=0 ------------(9)
ここに、Srは飽和度、C(ψ)は圧力水頭ψの関数としての比水分量で、C(ψ)=n(dSr/dψ)で与えられる(n:間隙率)。式(8)、(9)が不飽和領域へ拡張したBiotの多次元圧密方程式である。
境界条件は、
・変位既知境界(S1型)
・外力既知境界(S2型)
・水頭既知境界(Γ1型)
・流量既知境界(Γ2型)
の4種類があり、領域外部はS1型かS2型、およびΓ1型かΓ2型のいずれかの境界条件が課せられる。
このページのトップへ
地震継続時間中の間隙水圧および有効応力の取り扱い
地震終了後の間隙水圧の消散、浸透および応力〜変形解析は、地震終了時点でのFLIPの間隙水圧、有効応力を取り込み、これを初期値として通常の連成解析を行えば良い。
一方、地震継続時間中からの解析では、間隙水圧を図-1のように取り扱う。図-1(a)には、非排水条件下の解析であるFLIPの過剰間隙水圧を、同図(b)にはFLIPDISにおける過剰間隙水圧を示した。n-1ステップからnステップ間のFLIPにおける過剰間隙水圧の増分をPnとしている。FLIPDISのnステップにおいてこのPnを現在の間隙水圧に足し合わせると共に、これに伴う有効応力の変化を評価する。このようにして新たに得られた間隙水圧と有効応力を初期値として連成解析を行い、この操作を繰り返す。
ここで、Pnを足し合わせてとき有効応力の変化の評価法は重要である。拘束のない無限地盤中の要素であれば、σij'= σij'+(1/3)Pnδijで評価できるが、平面ひずみ条件も含めて拘束のある地盤中では、異方的に有効応力が変化する。本プログラムでは、FLIPにおけるn-1ステップからnステップ間の有効応力の変化分をFLIPDISに取り込んでいる。
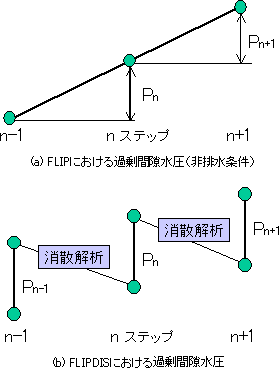
図1 地震継続時間中の過剰間隙水圧の評価法
このことは、地震応答による有効応力の変化も含めて評価したことになる。
本解析法と類似の解析として、等価線形化法・地震応答解析で得られる各要素のせん断応力時刻歴から過剰間隙水圧の発生量を評価し、間隙水圧の消散に伴う圧密解析と組み合わせた手法1)がある。ただし、関連文献に上で述べたPnを足し合わせてとき有効応力の変化の評価法については明記されていない。これは、この種の解析では間隙水圧の評価を優先させ、応力の異方性も含めた有効応力については簡易的な取り扱いをしているためと考えられる。
このページのトップへ
要素特性と時間積分
連成解析では、支配方程式をu-p形式により定式化するが、間隙水圧を要素で定義するCristianの方法と節点で定義するSandhuの方法がある。Cristian型は境界近傍の要素形状に精度が左右されることから、最近ではSandhu型が一般的になっているようであり、本解析でもこのタイプを用いている。
一方、FLIPの間隙水圧は要素で定義されていることから、変換プログラムにより節点での値に変換している。また、間隙水圧は応力と同じディメンションを持ち、応力は変位を1回微分したひずみと線形関係にあることから、変位の形状関数は間隙水圧の形状関数より1つ多い次数とすることが合理的であると言われている。従って、本解析でも変位に関しては2次要素を選択しているが、簡便さから1次要素の利用も可能にしている。
連成解析のみならず非定常解析では時間的な離散化が必要になる。時間的な離散化は、ガラーキン法と等価な手法を用いている。
このページのトップへ
土の構成式
本解析で使用できる土の構成式は、現在の所以下の3種類である。
①:線形弾性
②:平均有効主応力σm依存
③:間隙水圧比Rに基づく指数関数(上原ら2)の方法)
FLIPの解析で線形平面要素(IEL=3)と指定された要素はすべて、①(線形弾性)となる。マルチスプリング要素(IEL=9)と指定された要素は、①、②、③の選択が可能である。
②は現在の平均有効主応力σmの関数として、次式によりヤング係数Eを定義している。
E = E0(σm/σma)1/2 ----------(10)
ここに、σmaはFLIPで入力される基準平均有効拘束圧、E0はσm=σma のときのヤング係数である。本解析では、σma=98kPaに固定している。すなわち、FLIPの入力データはSI単位で定義し、σma=98kPaに固定しなければならない。ポアソン比および透水係数は一定としている。
③は次式で表される間隙水圧比Rを用いて、ヤング係数Eを定義しており、
R=1−σm/σm0 ---------(10)
σm0は初期状態(地震発生前)での平均有効主応力である。Eは次式で定義される。
E=E0(σm0/σma)1/2/(EXP(aR−b)+1.0) ---------(11)
ここに、a、bは入力パラメーターである。上原ら1)は、a=3.701、b=3.087を用いているが、両値を用いるとほぼ液状化した地盤(R≒1.0)では沈下量が②の結果と同程度かやや小さいものとなる。
通常の成層地盤では間隙水圧の消散による圧密沈下で土が破壊する場合は少ないと考えられるが、不整形な2次元問題あるいは粘性土層が介在するとき、土が破壊する場合も考えられる。この場合、圧縮側でモールクーロン型のせん断強度、引張側で引張強度を評価した破壊条件を考慮できるようにしている。また、間隙水圧の大規模な移動により2次元問題では大変形が生じる場合も考えられるため、計算ステップ毎に節点の座標値を更新する幾何学的大変形解析もできるようにしている。
このページのトップへ
不飽和領域の取り扱い
地下水面より上部の地盤は、一般に不飽和領域である。このため、地下水面より上部の地盤を完全に乾燥したものとみなし、間隙水圧に関する境界条件を強制的に地下水面で定義する従来の方法は、問題も多い。本プログラムでは、地下水面より上部の地盤を不飽和領域とみなして不飽和浸透流の解析も併せて行えるようにしている。
飽和〜不飽和浸透流の入力データとして、不飽和浸透特性は重要であり、不飽和土の工学的性質を議論する上でも必要なパラメーターである。しかし、その計測手法は複雑であり、原位置での測定手法も確立されていないため、我が国の土に対する不飽和浸透特性データの蓄積は極めて少ない現状にある。このような現状を鑑みて、本プログラムでは不飽和浸透特性の簡便な推定法として不飽和浸透特性を関数モデル(van Genuchtenモデル3))を用いて表現している。
このページのトップへ
参考文献
1) 西、金谷ほか:「地震時における基礎地盤の安定性評価(その1)―動的解析に基づく砂・砂礫地盤の安定性評価手法の開発―」、電力中央研究所報告、U86002
2) 上原精治ほか:「排水条件を考慮した液状化時の砂の体積圧縮係数について(その2)」、第33回地盤工学研究発表会、pp.723-724、1998.7(山口)
3) 竹下祐二、河野伊一郎、「不飽和浸透特性の推定方法とその適用性について」、地盤と建設、Vol.11、No.1、1993.
